Tenhle článek možná nepotěší naše školou povinné čtenáře – školní rok už skoro končí, prázdniny klepou na dveře a najednou tu je článek, jehož náplní bude matematika a výpočty. Ale neskládejte zbraně – kosmonautika je jako každá jiná přírodní věda postavená na pevných základech matematiky a kdo chce do jejích tajů proniknout hlouběji, ten se jejím výpočtovým zákoutím nevyhne. Na druhou stranu chápeme, že ne každý má na matematiku buňky a proto se budeme snažit, aby byly všechny výpočty důkladně vysvětlené. Tento článek je totiž součástí našeho nepravidelného seriálu „Pro začátečníky„, který se srozumitelnou formou snaží vysvětlit základy kosmonautiky. Pokud tedy chcete vědět, jak se počítá rychlost spalin, které upouští trysku raketového motoru, nebo co označuje zkratka TWR, čtěte dál.
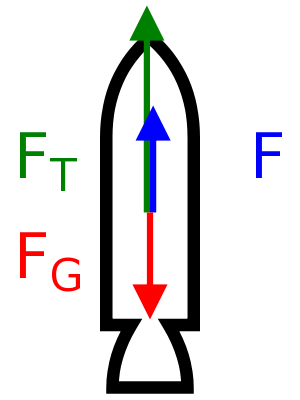
Jedním z mimořádně důležitých faktorů, které ovlivňují výkonnost rakety je poměr tahu vůči váze. Občas můžete narazit také na zkratku TWR, což vychází z anglického výrazu thrust-to-weight ratio. Tato hodnota vychází z druhého Newtonova zákonu, kterému se také někdy přezdívá zákon síly.
Jestliže na těleso působí síla, pak se těleso pohybuje se zrychlením, které je přímo úměrné působící síle a nepřímo úměrné hmotnosti tělesa.
Co to ale znamená pro nás? V definici zákona se mluví o síle, která na těleso působí – v našem případě jde o tah generovaný raketovým motorem. Tady ale narážíme na první komplikaci – tah raketového motoru závisí na tlaku okolního vzduchu – proto někdy můžete u raketových motorů najít dvě hodnoty – tah na hladině moře a tah ve vakuu. Druhá hodnota je vždy vyšší, protože částice opouštějící trysku nemusí bojovat s tlakem okolního vzduchu. Tlak vzduchu se ale s výškou mění a proto budou výsledky lehce ovlivněné touto chybou. Pojďme teď na reálný příklad. První stupeň evropské rakety Vega se jmenuje P80. Na něm jsou umístěné ještě další stupně, ale abychom naše příklady v tomto článku zjednodušili, zkusme si představit, že bychom na startovní rampu postavili čistě jenom motor P80.

První stupeň P80 váží v prázdném stavu 7 330 kilogramů, pojme však 88 365 kilogramů paliva
Zdroj: https://farm1.staticflickr.com
Jeho tah (F) na úrovni moře je 2 261 kN. Jeho hmotnost (M) je 95,695 tuny. Jelikož je kilonewton tisíc newtonů a tuna je tisíc kilogramů, nemusíme si lámat hlavu s převody jednotek a můžeme rovnou vypočítat zrychlení (A). Stačí jen sílu vydělit hmotností. V našem případě tedy 2261 / 95,965 = 23,56. Jednotkou je samozřejmě m/s2. Čím vyšší je hmotnost, nebo naopak čím menší je tah, tím menšího výsledku pochopitelně dosáhneme. Analogicky můžeme říct, že při vyšším tahu a menší hmotnosti dosáhneme většího zrychlení, což je logické.
Abychom ale mohli vypočítat TWR, musíme vzít do úvahy ještě jeden faktor – gravitaci. Berme její průměrnou hodnotu 9,8 m/s2 jako náš základ. Vydělíme tedy vypočítanou hodnotu zrychlení tímto číslem a dostaneme se na hodnotu 2,59 – právě tohle je hledaná hodnota TWR.
Nyní když známe poměr tahu vůči váze, můžeme se podívat na další důležitý faktor – Δv [delta vé], který označuje změnu rychlosti – v našem případě budeme počítat, jakou celkovou změnu rychlosti dokáže motor udělit – čili jak moc dokáže zrychlit. Předešlý výpočet nám ukázal, že motor P80 má zrychlení 23,56 m/s2. Znamená to, že po první sekundě letu bude mít rychlost 23,56 m/s? Z tabulek vyčteme, že stupeň P80 hoří po dobu 106,8 sekund. Má to tedy znamenat, že (opět pokud ignorujeme tření o atmosféru), že by stupeň měl po dohoření rychlost 2516,2 m/s? Že by stačilo vynásobit akceleraci časem hoření a měli bychom výslednou rychlost? Nikoliv. Tak snadné to není.
Při letu totiž raketa spaluje palivo a tím pádem klesá její hmotnost. A jak jsme si řekli už na minulých řádcích – čím je raketa lehčí, tím větší má akceleraci. Tah totiž zůstává stejný, ale hmotnost klesá. Tím se dostáváme k základní rovnici kosmonautiky. Rovnici, která nese jméno ruského učence Konstantina Ciolkovského (viz jeho životopis na našem webu). Ciolkovského rovnice umožňuje vypočítat, jaké rychlosti raketa dosáhne.
Co ale znamenají jednotlivé veličiny? Nalevo od znaku „rovná se“ máme Δv, což je hodnota, kterou již známe z našich minulých článků a kterou chceme vypočítat – jaká bude celková změna rychlosti za dobu hoření rakety. Hodnota ve je trochu specifická a budeme se jí muset věnovat podrobněji na dalších řádcích – udává totiž výtokovou rychlost plynů z trysky motoru. Další je symbol logaritmu a dostáváme se ke zlomku. Čitatelem je m0, což značí hmotnost rakety před zážehem.Jmenovatel je vyjádřen jako m1, což je hmotnost rakety po zážehu, v našem případě tedy po vypálení všeho paliva.
Jak ale vypočítáme rychlost vypouštěných plynů? Představme si startující raketu, jako systém, který se zbavuje části své hmotnosti. V tabulkách můžeme najít, že motor P80 pojme 88 365 kg paliva. Abychom celý proces zjednodušili, budeme ignorovat, že se rychlost spalování může měnit a budeme ji považovat za konstantní. Jelikož P80 hoří 106,8 sekund, pak za jednu sekundu spálí 827,39 kg paliva. Známe i tah rakety, tedy v našem případě 2261 kN. Aby se to dobře počítalo, můžeme převést kilogramy na tuny, nebo kilonewtony na newtony. My zvolíme první možnost a převedeme množství spáleného paliva za sekundu na 0,82739 tuny. Abychom vypočítali rychlost vyvržených plynů, vydělíme tah motoru hmotností spáleného paliva za sekundu – v našem případě tedy 2261 / 0,82739 = 2732 m/s. Spaliny tedy opouští trysku motoru P80 rychlostí téměř 3 kilometry za sekundu! Nyní můžeme všechny hodnoty dosadit do vzorce.
Po vypočítání dosáhneme výsledku 7019 m/s. Tato hodnota nám ukazuje, že pokud by naše planeta neměla atmosféru, pak by první stupeň rakety Vega dosáhl téměř orbitální rychlosti. V reálném světě tu samozřejmě máme atmosféru, která svým třením vše komplikuje a navíc chceme, aby raketa dopravila na oběžnou dráhu nějaký náklad. Proto potřebujeme další raketové stupně, které se zažehnou, až v P80 dojde všechno palivo.
Na závěr si dáme ještě jeden výpočet. A nebudeme troškařit – dáme si rovnou první stupeň americké rakety Saturn V, která umožnila pilotované cesty k Měsíci. Nejprve si vypíšeme všechny hodnoty, které budeme pro výpočet potřebovat.
Tah motoru F-1 na hladině moře = 6833 kN
Hmotnost plného stupně = 2 282 tun
Začneme tedy počítat a v prvním pokusu schválně uděláme chybu. Z těchto hodnot bychom vypočítali zrychlení – 2,99 m/s2. Poměr tahu vůči hmotnosti tedy vychází na 0,31. To ale na první pohled nedává smysl. Vždyť pokud má nosič TWR menší než 1, nemůže se zcela logicky odlepit od rampy. Kde jsme tedy udělali chybu? V zadání je tah jednoho motoru F-1 – první stupeň rakety Saturn V jich ale měl pět. Tím pádem je tah celého prvního stupně 5 x 6833, tedy 34 165 kN. Teď už nám rovnice bude dávat větší smysl – zrychlení vychází na 14,97 m/s2. Poměr tahu vůči hmotnosti nám potom ukáže 1,52. TWR je vyšší než 1 a raketa má dostatečný výkon na to, aby se odlepila od země. Povšimněte si ale že, zatímco u P80 nám TWR vyšel na 2,59, u prvního stupně Saturnu V je hodnota jen 1,52. To je matematické vyjádření toho, co můžeme vidět na záznamech startu rakety Saturn V – tento nosič se kvůli své masivní váze odlepoval od rampy jen velmi, velmi nerad a pomalu. Nezapomínejme na to, že my počítáme TWR pouze pro první stupeň, ale v reálu, měl tento nad sebou ještě další stupně! Abychom mohli ve výpočtu pokračovat, musíme si uvést další údaje.
Hmotnost pohonných hmot= 2 148,6 tun
Prázdná hmotnost = 133,4 tun
Doba hoření = 161 sekund
Jak jsme si již řekli, první stupeň Saturnu V měl 5 motorů. Na každý tak připadalo 429,72 tuny paliva. Pokud tuto hodnotu vydělíme dobou hoření, dostaneme se na spotřebu paliva 2,67 tuny pohonných hmot / sekundu na jeden motor! Celková spotřeba všech pěti motorů byla 13,35 tuny pohonných hmot / sekundu. Pokud vydělíme tah prvního stupně (34 165 kN) spotřebou paliva ze sekundu (13,35 tuny), dostaneme se k výsledku 2559 m/s. A nyní už nezbývá nic jiného, než dosadit všechny hodnoty do vzorce celkového Δv.
Výsledek je 7266 m/s. Jak je vidět, tak pokud by Země neměla atmosféru, tak by se na oběžnou dráhu nedostal ani samotný první stupeň gigantické rakety Saturn V. Skutečnost je samozřejmě komplikována nejen atmosférou, ale i dalšími stupni, které měl první stupeň nad sebou. Kdo by měl zájem, ten si může všechny hodnoty vypočítat i pro celou raketu.
P.S. Číselné hodnoty pro raketu Vega jsem čerpal z jejího oficiálního prezentačního dokumentu, hodnoty pro Saturn V jsem vyčetl v databázi SPACE 40.
Zdroje informací:
https://www.youtube.com/
https://cs.wikipedia.org/
http://wiki.kerbalspaceprogram.com/
http://www.arianespace.com/
http://www.lib.cas.cz/
Zdroje obrázků:
http://wiki.kerbalspaceprogram.com/…/300px-Gravity_turn_start.svg.png
https://farm1.staticflickr.com/358/18883064478_39b38bae1f_b.jpg
https://upload.wikimedia.org/…engine_being_transferred_to_the_test_stand.jpg
https://upload.wikimedia.org/wikipedia/commons/7/7e/Ap10-KSC-68C-7912.jpg

 25. června 2015
25. června 2015


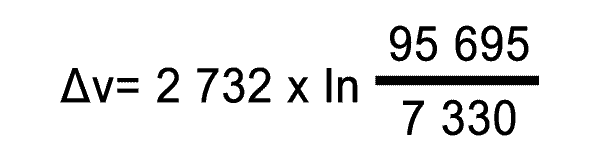

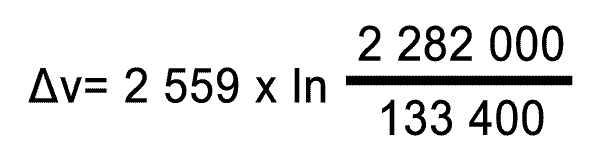


 Rubrika
Rubrika  Štítky:
Štítky: 













Skvělý článek, ale zajímali by mě dvě věci. Kde jste našli přesnou dobu hoření stupně P80. Wikipedie říká 110 s, ale kde najdu přesnou hodnotu a druhá otázka. Jak se počítá deltaV s více faktory jako např. Gravitace, tření. Předem děkuji za odpověď.
Hezký den,
díky za pochvalu. Jde o článek sepsaný před více než 4 lety. Bohužel není v mých silách dohledat (nebo si vzpomenout), kde přesně jsem vzal který údaj. Myslím si ale, že to bylo na webu spaceflight101, ale bez záruky.
K druhé otázce – tam vždy záleží na konkrétní situaci. Ale většinou se počítá nejprve s čistou situací tedy bez vnějších vlivů, které se tam pak mohou nějakými dalšími formami zohlednit.
Ahoj, mohl by mi někdo, prosím, jako nevzdělanci převést ty jednotky síly a tahu na jednotku pro mě pochopitelnou, něco jako horsepower nebo kilowat. Chtěl bych si to umět představit, jakou asi ty rakety mají sílu. Z matematiky jsem ani neodmaturoval :). Díky za vaši práci.
Ahoj,
Chtěl bych se zeptat jak by se to počítalo s atmosférou ?
Děkuji,
Kryštof
Už to tady zaznělo, ale dovolím si to trochu rozvést. Ciolkovského rovnice platí pro raketu, na niž nepůsobí žádné jiné síly kromě tahu motoru, takže počítat pomocí ní rychlost, jakou raketa dosáhne při startu ze Země, nejde (i když zanedbáme atmosféru, pořád tu máme tu zpropadenou gravitaci). Výsledek se prostě musí integrovat od startu až do konce.
Aby se úloha pro základní úvahy zjednodušila, dá se delta-v pro různé úlohy předpočítat. Např. pro dosažení nízké oběžné dráhy u Země je delta-v přibližně 9.4 km/s.
https://en.wikipedia.org/wiki/Delta-v_budget
Pak už samozřejmě v Ciolkovského rovnici ztrácí delta-v význam finální rychlosti rakety (při startu z nulové rychlosti), ale vyjadřuje jakousi „energetickou náročnost“, kterou musíme zohlednit při konstrukci rakety atd.
Zaujimavy clanok, ale mam jednu otazku: Sam autor pri vypocte TWR uvazuje posobenie gravitacie, ale v dalsom uz akosi na nu zabuda.
Uvedeny vypocet zmeny rychlosti by mal podla mna platit len v prazdnom priestore daleko od hmotnych objektov. Ak totiz tah motora udeluje zrychlenie a, a toto zrychlenie ma smer kolmo nahor (proti smeru gravitacneho zrychlenia g), tak vysledne zrychlenie motora bude a – g. V tych uvedenych prikladoch teda radovo 14 m/s^2. Mylim sa?
V Ciolkovskeho vzorci su veci samozrejme v poriadku, tam je zahrnuta velkost vytokovych plynov a najma hmotnost objektu.
Chvilku jsem pátral, kterou oblast máte na mysli a už jsem ji našel. Vy mluvíte o té pasáži, kde u P80 násobíme vypočítané zrychlení časem hoření, že? Myslel jsem si, že to nemusím rozvádět, když o chvíli později napíšu, že tento výpočet není správný.
No dalej je to rozvadzane, ale tam uz ides na vypocet uplne inym sposobom… Podla mna by toto bolo vhodne doplnit, ze to zrychlenie je znizene gravitacnym zrychlenim. Na takomto vypocte nie je principialne nic zle, plati ale len pre objekty, ktore nestracaju hmotnost (pri zanedbani odporu vzduchu).
Myslím, že poukazuje na to, že ciolkovskeho rovnice platí jen pro objekty, na které nepůsobí žádná další síla. Ani gravitace. Například na raketové saně na supraledě ve vakuu. Raketu startujici ve svislé poloze, která se prvních deset km probíji přes hustou atmosferu a celou dobu ji „brzdí“ gravitace, se takhle ani přibližně počítat nedá.
Ale moc dík autorovi za odvahu napsat aspoň tohle. Každý vzorec snižuje čtenost na půlku. 🙂
Rádo se stalo. Je fakt, že jsem dlouho přemýšlel, zda se do tohoto tématu pustit 🙂
Pěkný Dugi, ale přečti si to po sobě, je tam pár šotků 😉
Ach jo. Autor si dá práci s článkem a vždy se naje nějaký troll, co začne prudit. Kdyby měl mistr dokonalý snahu, tak tu ty šotky napíše nebo to pošle autorovi mejlem.
Nebyl bych až tak příkrý. Jsem rád, že čtenář upozornil na to, že jsou v článku chyby. Pokusím se je najít a opravit. Jsme rádi za každé upozornění na chybu – ať už je konkrétní, nebo obecné. 😉
Je trochu zvláštní počítat situace typu „pokud by Země neměla atmosféru“ s tahem na hladině moře při 100 kPa, ale což. 😉
To mi připomíná ten fór o fyzicích, kteří měli zaručit šéfům výhry v dostizích:
„Takže, začali jsme malým zjednodušením: každý kůň je vlastně dokonalá koule ve vakuu … “ 😀
LOL