Jelikož náš nedávný článek o základním rozdělení oběžných drah pro začátečníky sklidil velký čtenářský úspěch, rozhodl jsem se sepsat jeho volné pokračování. I dnes probereme základní součást kosmonautiky a budeme se přitom snažit psát všechno jazykem srozumitelným bez zbytečných technických termínů. Zkrátka a dobře – vysvětlíme si základní manévry na oběžné dráze tak, aby se v nich vyznal každý zájemce o kosmonautiku, který se v tomhle atraktivním oboru teprve rozkoukává.
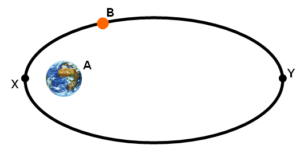
Hned na začátek si musíme ujasnit jednu základní věc – ačkoliv se často mluví o tom, že oběžná dráha nějakého tělesa je kruhová, není tomu tak. Všechny oběžné dráhy jsou totiž elipsy. Naprosto přesně kruhová dráha neexistuje, vždycky je tam alespoň drobná odchylka. Proto je lepší říkat, že je těleso na téměř kruhové dráze. Naopak dráhy, které jsou na první pohled výrazně protáhlé můžeme s klidným srdcem označovat jako eliptické.
Prvním termínem, se kterým se dnes seznámíme bude apsida. Je to pomyslný bod na oběžné dráze, ve kterém je družice (ať už přirozená nebo umělá) nejblíže nebo nejdále svému mateřskému tělesu. Každá oběžná dráha má tedy logicky apsidy dvě. První je určená pro bod, kdy je družice od tělesa nejdále. Ta se označuje předponou apo-. V obecném označení tedy apoapsida. Druhý bod leží na přesně opačné straně elipsy. Označuje místo, kde je družice naopak mateřskému tělesu nejblíže. Poznáme ji podle předpony peri-. V obecném případě tedy mluvíme o periapsidě.
Pro různá kosmická tělesa je samozřejmě možné místo obecných termínů apoapsida a periapsida možné použít specializované termíny vztažené přímo na konkrétní objekt.
Země – apogeum / perigeum
Měsíc – aposelenium / periselenium
Slunce – afélium (afel) / perihel(ium)
Venuše – apocytherion / pericytherion
Mars – apoareum / periareum
Jupiter – apojovium / perijovium
Saturn – apokronium / perikronium
Kromě již zmíněné vzdálenosti od mateřského tělesa mají apsidy ještě jednu důležitou vlastnost a tou je rychlost, kterou se těleso při průletu jimi pohybuje. V apoapsidě, tedy v nejvyšším bodě dráhy má družice nejmenší rychlost a naopak periapsidou, kdy je mateřskému tělesu nejblíže prolétá v největší rychlosti. Čím je oběžná dráha víc protáhlá, tím jsou rozdíly v rychlostech větší. Naopak u téměř kruhových drah jsou rozdíly minimální – třeba jen několik km/h.
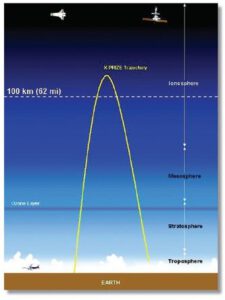
Žlutě vyznačená suborbitální dráha – v jejím nejvyšším bodě bychom našli apoapsidu.
Zdroj: http://www.examiner.com
Jak je to se suborbitální dráhou? Jak jsme si popsali v minulém díle našeho miniseriálu, je to taková dráha, při které těleso nedosáhne první kosmické rychlosti a neusadí se tedy na oběžné dráze. Když raketa spálí všechno palivo, letí družice setrvačností vzhůru, postupně ztrácí rychlost a nabírá výšku. Po dosažení apoapsidy se situace mění – rychlost se znovu začne zvyšovat a naopak výška klesá. Hezky česky řečeno – těleso začne po dosažení apoapsidy padat zpátky k Zemi. U suborbitální dráhy tedy neexistuje periapsida. Tedy, ona teoreticky existuje, jen je umístěna pod povrchem Země.
Teď si představme jinou situaci – družice prolétá apoapsidou a zažehne v ní své motory ve směru letu. Je jedno, zda přitom využije motory vlastní, nebo motory horního stupně rakety. Během tohoto zážehu se začne až doposud suborbitální dráha protahovat. Body dráhy, které se dotýkají Země (viz přiložený obrázek) se od sebe začnou vzdalovat. A pokud trvá zážeh dostatečně dlouho, potkají se na druhé straně planety – periapsida jakoby „vyskočí ze Země“ na druhé straně planety a stoupá nahoru.
Jak se tedy družici podařilo tzv. zakulatit svou oběžnou dráhu? Jen tím, že v apoapsidě zvýšila svou rychlost. Rychlost je totiž v orbitální mechanice alfou a omegou. Pokud chcete změnit svou oběžnou dráhu, musíte změnit svou oběžnou rychlost. Za další příklad si vezmeme třeba telekomunikační družici, která se má dostat na geostacionární dráhu. Nosná raketa ji vypustila na dráze přechodné ke geostacionární. Jak jsme si řekli minule, tato dráha je silně protáhlá a její apoapsida leží ve výšce geostacionární dráhy. Družice proto při průletu apoapsidou zažehne své motory, aby o kousek povytáhla své perigeum. Po několika průletech spojených se zážehy je nakonec družice na téměř kruhové geostacionární dráze. Neméně důležitá je samozřejmě i orientace Vaší lodi, tedy směr, kterým zážeh vůči trajektorii provedete.
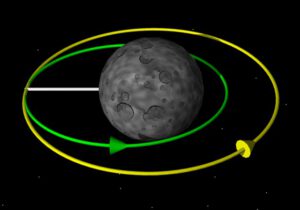
Snižování oběžné dráhy – žlutě je původní téměř kruhová a zeleně je vyznačená dráha po retrográdním zážehu
Zdroj: http://www.elwico.pl
Aby to bylo srozumitelnější, pomůžeme si dalším malým příkladem – v minulém případě družice zažehla své motory ve směru letu aby zakulatila svou oběžnou dráhu – zvýšila tedy svou rychlost. Nyní si představme loď, která krouží na oběžné dráze kolem Země a potřebuje se vrátit na planetu. Pro příklad nemusíme chodit daleko – stačí si vzpomenout na návraty z oběžné dráhy v podání raketoplánů, nebo ruských lodí Sojuz. V takovém případě se loď obrátí proti směru letu (tzv. retrográdním směrem). Když zažehne své motory, začne na oběžné dráze zpomalovat. Tím pádem její periapsida klesá dolů a jakmile se dostane do výšky, kde už má Země svou atmosféru, znamená to, že se loď vrátí domů. Stačilo se otočit čelem vzad, zážehem snížit svou rychlost a to se hned odrazilo na umístění periapsidy.
Pro lepší zapamatování si tedy pamatujme, že pokud družice provede zážeh v periapsidě, ovlivní tím polohu apoapsidy a naopak. Zážeh v apopasidě může zvýšit nebo snížit polohu periapsidy. Retrográdní zážeh (proti směru letu) rychlost snižuje a polohu protilehlé apsidy také snižuje. Naopak zážeh ve směru letu rychlost zvyšuje a stejně tak zvyšuje i polohu protilehlé apsidy.
Další možností, jak provádět manévry na oběžné dráze je změna sklonu oběžné dráhy. V takovém případě se zážeh neprovádí ani ve směru letu (tím by se oběžná dráha zvyšovala), ale ani ve směru opačném (tím by se snižovala). Pokud je potřeba změnit sklon dráhy vůči rovníku, musí se družice otočit kolmo ke směru letu. Zkusím to k něčemu přirovnat – když si lehnete na zem a roztáhnete ruce do kříže, pak vaše hlava míří ve směru letu, nohy proti směru letu. Vaše ruce jsou kolmé ke směru letu. A stejné je to i s družicí na oběžné dráze. Pokud potřebuje změnit sklon oběžné dráhy vůči rovníku, otočí se buďto k levé, nebo k pravé ruce. Kterou si vybere záleží na tom, jestli chce sklon zvýšit, nebo snížit.
Tyto manévry jsou mimořádně náročné na spotřebu paliva a provádí je především družice vynášené na geostacionární dráhu. Když startují od rovníku (třeba z kosmodromu v Kourou), mají už od začátku malý sklon k rovníku a proto provádí jen minimální korekce. Geostacionární dráha má, jak jsme si minule řekli, sklon dráhy vůči rovníku 0°. Naopak pokud družice startuje z ruských kosmodromů, které jsou daleko od rovníku, má po startu velký sklon k rovníku a musí provést řadu zážehů, než se jí podaří sklon snížit na požadovaných 0°.
Na závěr si musíme říct, že zatímco v případě zážehů ve směru nebo proti směru letu je to jednoduché, protože se směr našeho zážehu nemění, u zážehů kolmých k dráze letu, tedy u zážehů, které mění sklon oběžné dráhy je situace jiná. Zkuste si to představit – družice se otočí o 90° proti směru letu, zažehne motory a změní sklon dráhy vůči rovníku o řekněme 5°. Co to ale znamená? Že už není proti směru letu otočená o požadovaných 90°, ale buďto o 85°, nebo o 95°. Družice proto musí provádět řadu drobných korekčních zážehů, které korigují provedené změny dráhy a zajišťují, aby byla stále otočená o 90° proti směru letu.
Doufám, že se začátečníkům tento díl líbil a že z něj pochopili základní zákonitosti pohybu na oběžné dráze. Téma jsem se snažil maximálně zjednodušit, ale i přesto je potřeba mít poměrně dobrou představivost. Na závěr článku mi proto dovolte, abych Vám doporučil počítačovou hru Kerbal Space Program (demo je na oficiálních stránkách ke stažení zdarma). V této hře si budete moci všechno sami vyzkoušet – na vlastní oči uvidíte, jak je to s apsidami, vyzkoušíte si snižování a zvyšování oběžné dráhy, zkrátka všechno, o čem byla v tomto článku řeč.
Zdroje informací:
http://cs.wikipedia.org/
http://en.wikipedia.org/
http://en.wikipedia.org/
Zdroje obrázků:
http://upload.wikimedia.org/wikipedia/commons/0/02/Perigeum_apogeum.png
http://www.examiner.com/images/blog/EXID10722/images/trajectoryXP.jpg
http://www.elwico.pl/~ender-sz/orbiter-pdf/instrukcje/rsfd/img/Orbit_diag_5.jpg
http://i853.photobucket.com/albums/ab99/dgatsoulis/ejectorientation.jpg

 18. února 2013
18. února 2013







 Rubrika
Rubrika  Štítky:
Štítky: 













Tyto webove stranky jsem objevil pouze pred nekolika dny – nasmerovali nas sem z TECHNETU na idnes. Najde tu clovek odpovedi na vsechny nejasnosti,zabyvate se vsim. Co se tyce ale vyctu tech manevru na obezne draze, tak tam vam chybi jeden ze zakladnich. Tim je SETKANI NA OBEZNE DRAZE. Je to velmi komplexni manevr a i v knihach se mu vyhybaji. Neni o tom ani v clancich o Gemini, ani o Soyuzech. Rozumim, ze obe telesa musi obihat ve stejne rovine. Potom se musi dostat identickou drahu. Potom musi jeden druheho dohnat. A dozene jej pouze tak kdyz pribrzdi a sestoupi na nizsi drahu. A tady to zacina byt velice komplikovane. O setkani Apollo – Soyuz toho kdysi bylo napsano moc, tohle ale nikdy nikde nepopsali. Dokonce ani zde na Kosmonautix jsem odpoved na tuhle proceduru nenasel !
Nemohl by se nekdo pokusit o vysvetleni, konecne ? Dekuji, Josef,
Tento článek je určený naprostým začátečníkům, aby se přehledně dozvěděli, jaký vliv má změna rychlosti na polohu apsid, nebo jak se mění sklon oběžné dráhy. Pro složitější manévry zde není místo, což je případ právě setkávání na oběžné dráze, které patří (jak správně píšete) mezi komplexní manévry.
Rád Vám ale odpovím takto v komentáři. Částečně jste to už nakousnul sám. Dejme tomu, že máme stanici ve výšce 400 kilometrů a chceme k ní připojit zásobovací loď. Raketa ji vynese na nižší dráhu, která je stejně skloněna vůči rovníku a tak, aby byly roviny obou drah shodné. Jelikož je loď na nižší dráze, trvá jí oběh kolem Země o něco kratší dobu. Postupně tak stanici dohání. Postupně začne s využitím vlastního motoru zvyšovat svou oběžnou dráhu, takže se ke stanici začne přibližovat i z hlediska „výšky“. Tím, že loď vystoupí na trochu vyšší dráhu (která je však stále pod dráhou stanice), tak lehce zpomalí. Díky tomu se sníží rychlost přibližování ke stanici. A takhle to jde postupně dál a dál. V určité fázi se loď dostane do blízkosti stanice, kdy může navázat obousměrnou komunikaci, při které si obě tělesa začnou vyměňovat informace o poloze, orientaci, vzdálenosti atd. V této fázi, kdy oba objekty dělí už třeba jen dvacet kilometrů, jsou loď i stanice na oběžné dráze ve stejné výšce a obíhají tedy kolem Země stejně rychle. V této fázi už se začne loď přibližovat ke stanici, která udržuje svou orientaci přímo. Stále na ni samozřejmě působí změny rychlosti, které lehce mění oběžnou dráhu, ale na takto krátkou vzdálenost už to není moc podstatné. Loď se přibližuje k ose dokovacího uzlu a s pomocí zaměřovacího terče provádí revizi zda je správně v ose. Korekční trysky se starají o drobné korekce, které kromě jiného eliminují negativní vlivy předchozích změn rychlosti na oběžnou dráhu. Důležité je, že tyto změny jsou už jen velmi drobné.
Domnívám se, že se vám ho nepodaří v žádné astronomické literatuře najít.
Po detailním porovnání výsledků obou klíčových slov Vám dávám za pravdu. Článek jsem upravil, aby obsahoval častěji používanou verzi.
U Slunce se nepoužívá výraz apohelium/apohel, ale aphelium/aphel , nebo česky afélium/afel. Zrovna tak se to uvádí i v uvedených odkazech.
Nejsem si jistý, ale mám dojem, že se připouští obě varianty.
Tak jsem se náhodou dostal k tomuhle článku. Celkem přehledný a jednoduchý, pochvala autorovi. JEBEDIAH KERMAN ŽIJE! 🙂
Díky, jsem rád, že se Vám článek líbí 😉
Ano díky tomuhle článku jsem i já pochopil základy kosmonautiky. Nikdy se mi nedařilo dostat Jebediaha na orbitu, vždy jsem se buď dostal, že jsem měl periapsidu na km což je málo a spadl jsem. Ještě by jste zde mohl vysvětlit jak se používá gravitace ke zrychlení k cestě na Měsíc. Jestli jsem pochopil správně tento článek, mělo by to být zjednodušeně tak, že v periapse ve směru letu zažehnu a mělo by mě to vyhodit směrem k Měsíci 🙂 Díky moc za tenhle článek
Těší mne, že je Vám článek užitečný. S letem na Měsíc máte pravdu. Stačí v periapsidě zažehnout motor ve směru letu a vytáhnout apoapsidu do dostatečné výšky. K tomu, abyste na Měsíc doletěl potřebujete, aby byl Měsíc tam, kde má být, ve chvíli, kdy budete u apoapsidy. Pak si Vaši loď už Měsíc sám přitáhne svou gravitací. Pak je samozřejmě potřeba dráhu u Měsíce zakulatit – zpětným zážehem v periapsidě.
Dobrý den! Rád bych se zeptal na jednu věc, kterou jsem už potrápil mnoho lidí, ale nikdo mi odpověď nedal 🙂
Představme si raketu, která má neomezenou zásobu paliva, ale nikdy nedosáhne první kosmické rychlosti – může se jí jen přiblížit. Je možné se s touto raketou dostat na oběžnou dráhu nebo se bude vždy jednat jen o dráhu suborbitální?
Díky moc.
Dobrý den, rozhodně se nebude jednat o dráhu orbitální, protože těleso bude v pohybu díky působení motorů. Raketa bude kroužit kolem Země, ale pokud by svůj motor vypnula, půjde k zemi. Je to ostatně podobné jako když letí letadlo – má určitou rychlost, ale jakmile vypne motory, půjde k zemi. Ovšem nazývat takovou dráhu suborbitální není úplně vhodné. Nejlepší by bylo vymyslet pro ni nějakou třetí kategorii mezi suborbitální a orbitální dráhou, ale jelikož se jedná pouze o hypotetickou úvahu, není vymýšlení nového termínu potřebné.
Ale abych odpověděl na základní otázku – taková raketa by mohla kroužit okolo Země po něčem, co by evokovalo oběžnou dráhu, ale skutečná oběžná dráha by to nebyla. Teď mě napadlo hodně pěkné přirovnání – představme si oběžnou dráhu jako elipsu okolo Země, která se jí nikde nedotýká. Suborbitální dráha má tvar kuželosečky, přičemž obě ramena se dotýkají Země – z jednoho „ramene“ se startovalo, raketa prošla vrcholem a druhým ramenem spadla k Zemi. Vám popisovaný případ by vypadal tak, že by se tato kuželosečka pohybovala podél Země – Samotná raketa (umístěná v jejím vrcholu) by opisovala elipsu podobnou oběžné dráze, ale vlastní působení sil by pořád připomínalo suborbitální dráhu. Od téí by se ale lišila v tom, že by se tato kuželosečka i se svými rameny neustále posouvala po povrchu Země s tím, jak by raketa letěla.
Doufám, že jsem to nepopsal moc složitě.
Díky! Jedna z mých „základních otázek života, vesmíru a vůbec“ je zodpovězena… 🙂
Dik za typ na Kerbal space, vcera jsem si s tim hral do 4 do rana a nemuzu se toho nabazit. Uz umim na hulvata poslat raketu na orbit. Ted jeste to udelat s minimalni spotrebou. Existuje nejaka idelani draha (urcite existuje) spis jak ji zjistit, jak dlouho kolmo nahoru a po jake krivce zahybat az na obeznou drahu ?
Je to hodně o citu. Pokud máte raketu, která „mete ostošest“, můžete udělat první náklon od podélné osy třeba už v 5 000 metrech, nebo i dříve, za zlatý střed já osobně považuju letět 15 000 metrů kolmo vzhůru a v této výšce se od svislé osy odchýlit cca. o 5 – 10°. Takhle chvilku letět a ve výšce 20 000 metrů se zase o 5° naklonit. Někde kolem 30 – 40 000 metrů nad planetou můžete už mít sklon 45° a nad 50 000 metry už leťte se sklonem 90°, tedy rovnoběžně s planetou. V té chvíli už by měl mít váš stroj dostatečnou výškovou rychlost a tak můžete využít tahu k tomu, abyste zakulatil dráhu. Atmosféra Kerbinu (planety) začíná cca 70 000 metrů nad povrchem. Pokud tedy budete mít apogeum ve výšce 75 – 80 kilometrů, můžete být v klidu. Pokud ne, nepokládejte ještě raketu do kolmého směru a nechte ji letět pod úhlem 45°, dokud apoapsida nedosáhne těch 75 km, pak můžete raketu položit. Ale všechna tahle čísla jsou ohromně individuální a nemusí sedět na každou raketu! Proto raději všechno otestujte. Držím palce 😉
Zdravím. ja osobne považujem let kolmo hore za stratu paliva. Veď aj skutočné rakety letia kolmo iba pár chvíľ a hneď sa nakláňajú.Ja nakláňam už v piatich kilometroch asi o 5 stupňov. Potom po prechode do redšej atmosféry nad 10 km už dávam náklon CCA 30-50 stupňov v závislosti od rakety a keď máte apoapsidu vo výške 50km, pokojne môžete raketu nakloniť horizontálne. Apoapsida vám bude rásť aj tak. A navyše, vo výške 50 km už je veľmi riedka atmosféra a kratší let v nej sa na rýchlosti moc nepodpíše.
Super. Velmi dobre citanie, aj prvy diel.
Mal by som este jeden navrh na clanok, ktory by som si rad precital – co takto vysvetlit princip raketoveho motora (a naozaj do detailu, vratane typov paliva, a preco je take a preco nie je onake atd..)?
Dam tu jednu naivnu otazku ako headline:
Preco vidim z rakety slahat plamene, ked vsetci predsa vidime, ze na uplne rovnakom principe poletujuci prepichnuty balon ziadne plamene nevypusta, iba plyn?
Dobrý den, díky a pochvalu. Článek o různých palivech chystám. Na Vaši otázku – je to jednoduché, protože balónek je v podstatě když to zjednoduším jen “hloupý sklad vzduchu” Nic s ním nedělá – Vzduch se do něj nahustí a pak se vypustí ven. Jenže v případě raketového motoru se palivo z nádrží spaluje – to jsou právě ty plameny a dým, které šlehají z rakety.
No a detailny, podrobny clanok na tuto temu by som si veru rad precital. A dodam podotazku: Nestacilo by pri ceste ‚hore‘ nejaky plyn nahustit a nechat ho vyfucat? Samozrejme, nemyslim balonik, ale uz nieco technicky silnejsieho.
Osobne predpokladam, ze asi nestacilo, ale o tom to je… najzaujimavejsie clanky (dokonca by som si dovolil povedat, ze objavy) vznikaju z tych najjednoduchsich otazok, ktore si polozime.
Ale ok, tesim sa na clanok, len by nemusel byt iba o palivach, ale aj o motoroch. Priznam sa, cital som na wiki o motoroch raketoplanov, a mal som z toho hokej v hlave 🙂
Pokusím se něco sepsat. Možná už na příští týden.
K dotazu – to by určitě nestačilo. Rakety váží mnoho desítek tun. Je potřeb je urychlit na rychlost téměř 8 km/s! Na to žádný nahuštěný plyn stačit nemůže. Už jenom z prosté úvahy – čím vyšší tlak bychom potřebovali, tím by musely být stěny silnější, aby tlaku uvnitř odolaly. Silnější stěny = vyšší váha = nižší nosnost. Zato chemická paliva v sobě ukrývají mnohem větší energii, která se jejich spálením uvolní. Momentálně neexistuje žádná metoda, která by mohla pro cestu atmosférou nahradit motory založené na chemické reakci, tedy hoření.